[알고리즘 정리] DP(Dynamic Programming) : 동적 계획법

✔️ DP(Dynamic Programming) 정의

DP(Dynamic Programming) 이란?

다이나믹 프로그래밍은 하나의 큰 문제를 여러 개의 작은 문제로 나눈 다음, 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용한다. 

 

✔️ DP를 쓰는 이유

DP는 일반적인 재귀(Recursion) 방식과 매우 유사하다.

큰 차이점은 일반적인 재귀의 경우 큰 문제를 작은 하위 문제로 나누어 해결하는 방법으로, 작은 문제들이 여러번 반복(중복 계산)되어 비효율적인 계산이 될 수 있다.

반면에, DP는 작은 하위 문제들로부터 시작하여 그 결과를 저장하고 이를 이용하여 큰 문제를 해결한다.

즉, DP는 재귀적 호출에서의 중복 계산을 방지하고 계산 속도를 향상시킨다.

 

✔️ DP 기법을 적용시킬 수 있는 조건

1. 중복되는 부분 문제(Overlapping Subproblems)

• DP는 문제를 쪼개고 그 하위 문제의 결과 값을 1) 저장하고, 2) 사용하여 전체 답을 구한다. 
• 피보나치 수열을 예시로 들어보자 ! 

출처 : https://velog.io/@boyeon_jeong/%EB%8F%99%EC%A0%81%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming

 

일반적인 재귀의 경우, f(3),f(2),f(1)은 동일한 부분 문제가 중복되어 나타난다. 

반면에, DP에서는 하위 문제의 결과 값을 저장해두기 떄문에 저장된 값을 재활용할 수 있다.

 

2. 최적 부분 구조(Optimal Substructure)

• 부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우 사용이 가능하다. 

출처 : https://hongjw1938.tistory.com/47

   예를 들어, A-B 까지의 가장 짧은 경로를 찾고자 하는 경우, 중간에 X가 있을 때, A-X/X-B 가 많은 경로 중 가장 짧은 경로라면 전체 최적 경로도 A-X-B 가 정답이 된다. 

 

 

✔️ DP 풀이 종류 

1. Bottom-Up

작은 문제부터 차근차근 해결해서 큰 문제의 해를 구하는 방법이다. 

보통 for문으로 문제를 해결하며 재귀 호출이 없어 시간과 메모리를 절약할 수 있다.

 

2. Top-Down

큰 문제부터 작은 문제로 내려가면서 큰 문제의 해를 구하는 방법이다. 

보통 재귀를 이용해 문제를 해결하며, 재귀를 실행하면서 전에 계산해둔 값이 있으면 계산을 생략한다. 

 

 

 

✔️ DP 알고리즘 적용 예시

백준 1463번 1로 만들기 문제이다. 

 

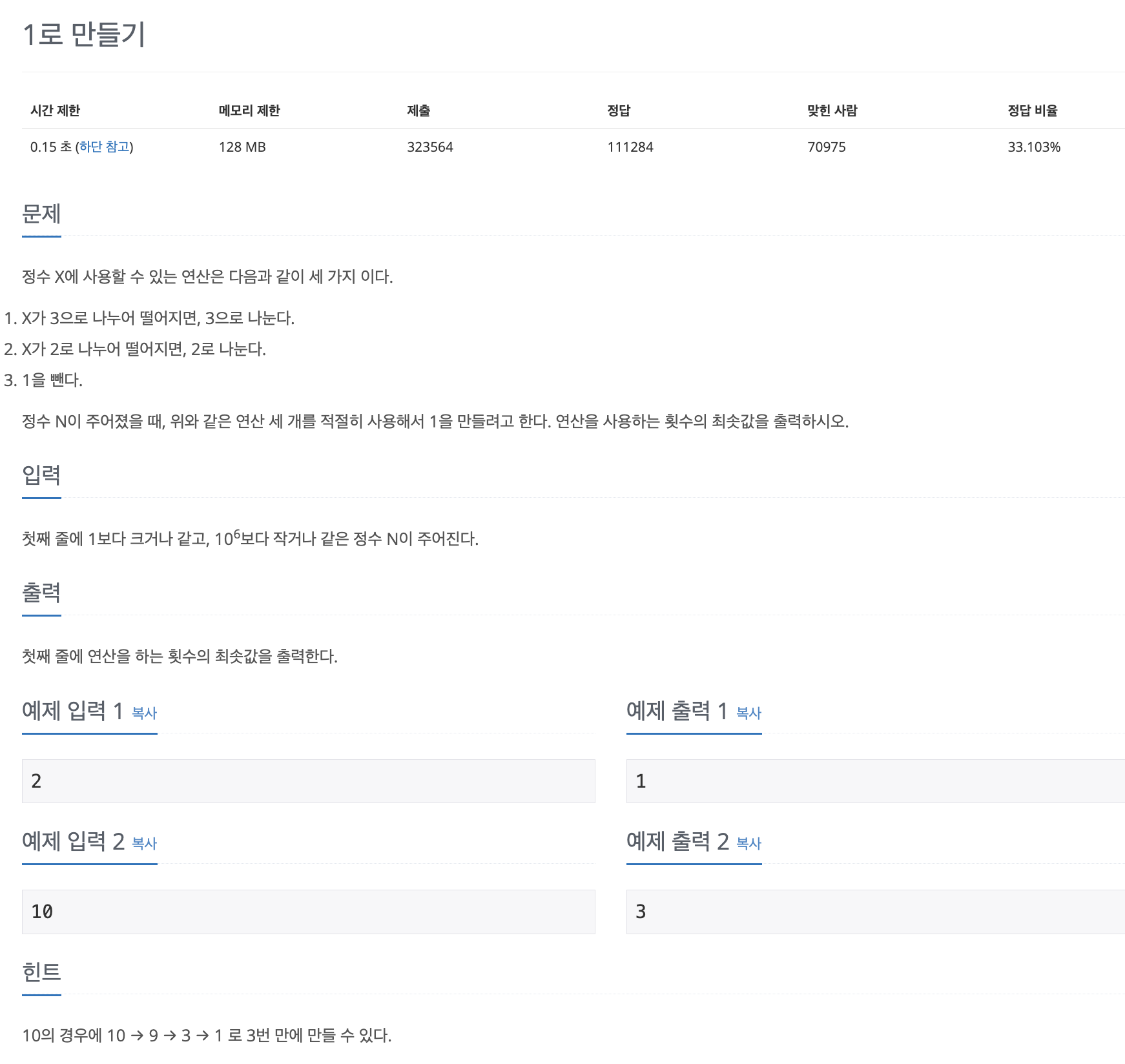
1. 어떤 흐름으로 답이 구해지는지 탐색하기 

• 4->2->1, 4->3->2->1, 4->3->1
• 3->1, 3->2->1
• 2->1

2. 큰 문제의 답에 작은 문제의 답이 포함 되는가? (재귀 인가?)

• YES
• 4->1 이라는 큰 문제는 3->1, 2->1 의 최소 연산 횟수를 구하는 작은 문제로 나누어짐. 

3. 하위 문제의 계산이 반복되나? (한 번 계산한 답을 이후에도 사용해야되나?)

• YES
• 4->1 의 최소 연산 횟수는 2->1의 최소 연산 횟수, 3->1의 최소 연산 횟수를 알아야 함.
• 3->1 의 최소 연산 횟수는 2->1의 최소 연산 횟수를 알아야 함. 

4. 그리디 인가?

• NO
• 그리디면, 2나 3으로 나눠질 때는 무조건 3으로 / 2로 나누어질 때는 무조건 2로 나누는 걸 반복하면 답이 나옴
• 반례) 10->9->3->1 (DP) / 10->5->4->2->1 (그리디) 

 

✔️ 문제 풀이 과정 예시

1. 반복되는 부분 찾기 

5->4->2->1                               4->2->1                           3->1                         2->1

5->4->3->2->1                        4->3->2->1                   3->2->1

5->4->3->1                               4->3->1

작은 문제의 답이 반복된다. 

 

2. dp 테이블 dp[i] 의미 정의

dp[i] = i 를 1로 만들기 위한 최소 연산 횟수

 

3. 점화식 세우기 

10->1 의 최솟값 = (9->1의 최소 연산 횟수 +1, 5->1의 최소 연산 횟수 +1)의 최소값

12->1 의 최솟값 = (11->1의 최소 연산 횟수 +1, 6->1의 최소 연산 횟수 +1, 4->1의 최소 연산 횟수 +1)의 최소값

...

=> dp[i] = min(dp[i-1]+1, dp[i/2]+1, dp[i/3]+1)

 

 

#참고

https://velog.io/@dlgosla/%EA%B0%9C%EB%85%90-%EC%A0%95%EB%A6%AC-%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95DP-Dynamic-Programming

https://velog.io/@boyeon_jeong/%EB%8F%99%EC%A0%81%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming

https://hongjw1938.tistory.com/47