728x90
✔️ 이분탐색(이진탐색) 이란?
이분탐색이란 오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다.
처음과 마지막의 중간값을 선택하여, 찾고자 하는 값과 크고 작음을 비교하는 방식을 반복하여 탐색을 진행한다.
따라서, 필수조건은 리스트가 오름차순으로 정렬되어야만 한다.
그림으로 이분탐색에 대해서 더 자세히 알아보자 !
0.
길이가 10인 오름차순으로 정렬된 배열이 있다고 하자. 31 이란 특정한 값의 위치를 찾고자한다.
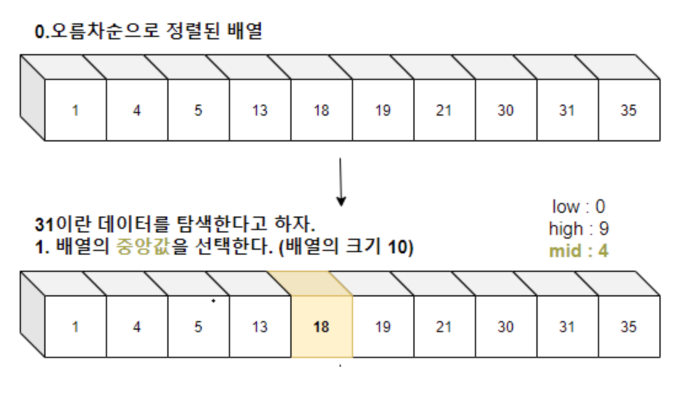
1.
먼저 low, high, mid 값 설정한다.
- low : 최소값의 인덱스
- high : 최고값 인덱스
- mid : 중간값 인덱스

2.
설정된 중앙값(mid)가 31보다 작으므로, low의 인덱스를 mid+1로 설정하여 우측을 선택한다.
(만약 중앙값(mid)이 31보다 큰 경우라면, high 인덱스를 mid-1로 설정하여 좌측을 선택한다.)
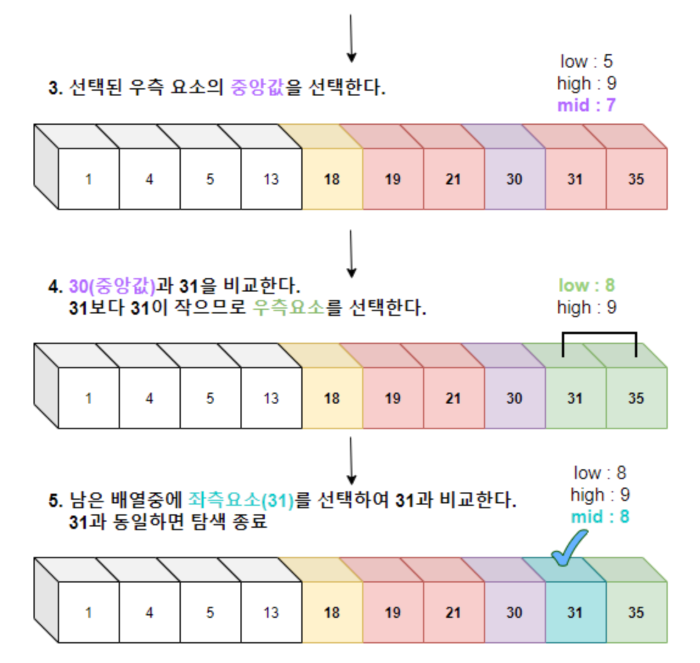
3~5.
위의 1~2번 탐색 과정을 답을 찾을 때까지 반복함. ( 단, low가 high 보다 커지는 경우 탐색은 종료됨.)
이분탐색 코드
import java.util.Arrays;
public class Main{
public static void main(String[] args) {
int[] arr = new int[] {31,18,5,4,19,35,1,13,30,21};
//반복문을 이용한 이진탐색
binarySearch_loop(arr, 31);
//재귀를 이용한 이진탐색
binarySearch_recursive(arr, 0, arr.length-1, 31);
}
public static int binarySearch_loop(int[] arr, int target) {
Arrays.sort(arr); // 0번 과정 : 오름차순 정렬
int low = 0;
int high = arr.length-1;
int mid = 0;
// low가 high보다 커지면 탐색 종료
while(low <= high) {
mid = (low + high) /2; // 1번 과정 : 중앙값 찾기
if(arr[mid] == target) {
return mid;
}else if(arr[mid] > target) { // 현재의 중앙값보다 작으면,
high = mid-1; // 왼쪽요소를 선택하기 위해 high = mid -1로 설정
}else {
low = mid+1; // 현재의 중앙값보다 크면, 오른쪽 요소를 선택하기 위해 low = mid+1로 설정
}
}
// 탐색해도 결과가 없는 경우
return -1;
}
public static int binarySearch_recursive(int[] arr, int low, int high, int target) {
Arrays.sort(arr); // 0번 과정 : 오름차순 정렬
if(low > high) {
return -1;
}
int mid = (low + high) /2; // 1번 과정 : 중앙값 찾기
if(arr[mid] == target) {
return mid;
}else if(arr[mid] > target) {
return binarySearch_recursive(arr, low, mid-1, target);
}else {
return binarySearch_recursive(arr, mid+1, high, target);
}
}
}
참고 자료
https://velog.io/@ming/%EC%9D%B4%EB%B6%84%ED%83%90%EC%83%89Binary-Search
728x90
'Coding Test > 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] 백트래킹이란? & 대표 문제: 백준 15679 N과M(1) - 자바 (0) | 2024.10.01 |
|---|---|
| [알고리즘] LIS : Longest Increasing Subsequnce 알고리즘 - DP 활용(최장 증가 부분 수열) (3) | 2024.08.28 |
| [알고리즘 정리] DP(Dynamic Programming) : 동적 계획법 (1) | 2024.08.24 |
| [알고리즘] 그리디 알고리즘(탐욕법) 정리 (0) | 2024.08.20 |


