LIS (최장 증가 부분 수열)란, 주어진 수열에서 오름차순으로 정렬된 가장 긴 부분 수열을 의미한다.
예를 들어, 아래의 그림처럼 수열 {10, 50, 20, 30, 10, 60} 이 있을 때,
만들 수 있는 증가하는 수열은 { 10, 50, 60 } 그리고 { 10, 20, 30, 60 } 이다. (이때, 꼭 등차수열이거나 순서가 연속적일 필요는 없다.)
이때, 가장 긴 증가하는 부분 수열(LIS)은 { 10, 20, 30, 60 } 임을 알 수 있다.
백준 11053번의 가장 긴 증가하는 부분 수열 의 예시로 알고리즘을 설명하겠다.
https://www.acmicpc.net/problem/11053
1. DP 테이블 정의하기
수열의 크기가 n인 배열이 입력으로 주어지면, 우리는 i 번째 원소의 LIS의 값을 부분 문제로 생각해볼 수 있다.

즉, dp 테이블의 원소 값 dp[i] 는 배열 arr의 i 번째 원소인 arr[i]의 LIS 값을 의미한다.
[ 원소 arr[0] = 10 ]
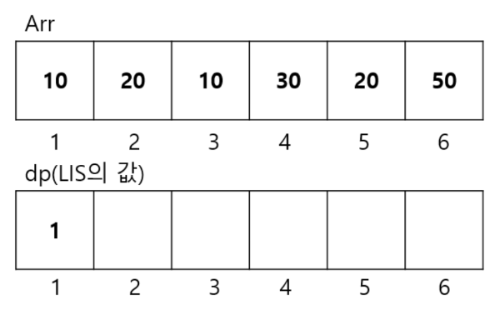
첫 번째 원소 10 의 경우, 이전의 원소가 없기 때문에 LIS 값은 자기 자신의 길이인 1이다. 즉, i = 0 일때 LIS는 {10} 인 셈이다.
[ 원소 arr[1] = 20 ]
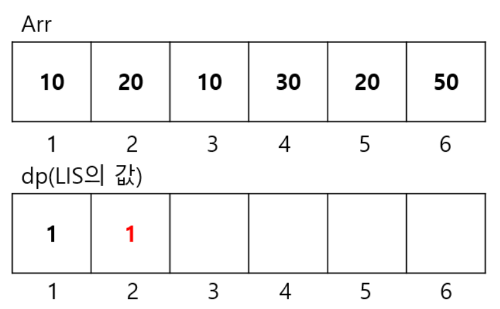
먼저, dp 테이블의 원소를 자기 자신의 길이인 1로 초기화 해준다. 수열 원소 중 자기 자신 밖에 없는 경우(가령, {20})는 1이므로, dp의 원소 값의 최솟값이 1이란 것을 알 수 있다. 이로부터 우선 해당 테이블의 원소에 dp 값을 채울 때 원소의 값을 1로 초기화할 수 있음을 유추해볼 수 있다.
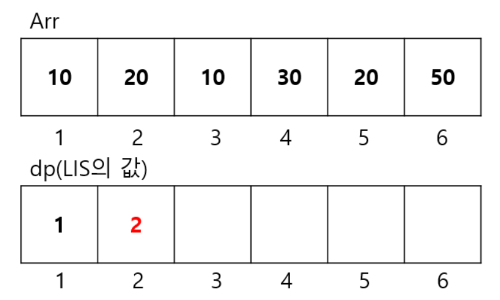
두 번째 원소 20 의 경우, 이전 원소인 10에 비하여 증가하는 상태 이므로 i = 1 일때의 LIS는 {10, 20} 으로 dp[1]은 2이다.
[ 원소 arr[2] = 10 ]
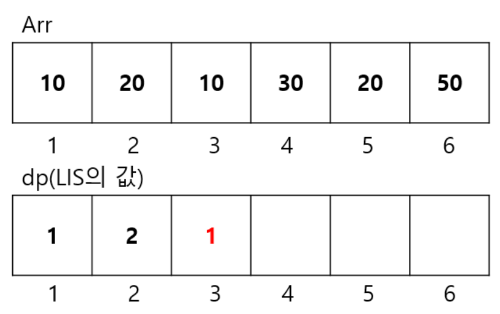
마찬가지로 원소 10 ,본인의 길이인 1로 dp[2] 값을 초기화 시켜준다.
세 번째 원소 10의 경우, 이전 원소들인 10, 20에 비해 증가하지 않는 상태이다. 따라서 자기 자신인 {10}이 LIS 가 되므로 dp 값은 1로 그대로 놔둔다.
[ 원소 arr[3] = 30 ]
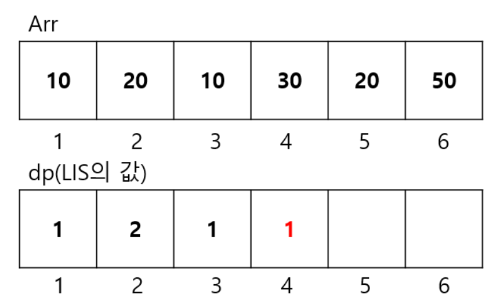
마찬가지로 원소 30 ,본인의 길이인 1로 dp[3] 값을 초기화 시켜준다.
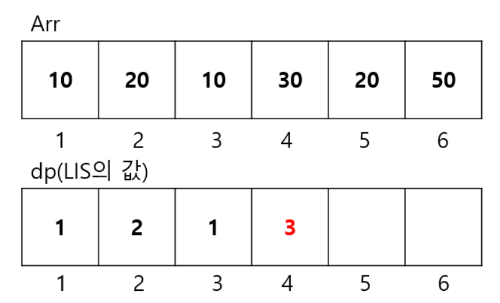
세 번째 원소 30의 경우, 이전 원소들인 10, 20에 비해 증가하는 상태이다. 즉, {10,20,30} 으로 증가된 부분 수열을 이룰 수 있다.
해당 dp값(=LIS 길이) 은 3인 것을 직관적으로 이해할 수 있다.
이 과정을 비추어 볼 때, 규칙성을 파악할 수 있다.
세 번째 원소 30의 경우를 생각하보면, 이전 원소들이 (10, 20, 10)에 비해 큰 값을 가지고 있으므로, 앞선 원소들 뒤에 추가 되면 최장 증가 부분 수열을 만들 수 있다.
즉, 해당 위치에서 앞 원소들에 비하여 증가할 가능성이 존재한다면, 해당 위치의 LIS의 값에 자기 자신의 길이를 +1 해주면 된다는 것을 파악할 수 있다.
자기 자신의 길이인 1로 초기화부터 생각해보자.

우선 첫 번째 원소 10보다 30이 크므로, LIS ( {10,30} )을 만들 수 있다.
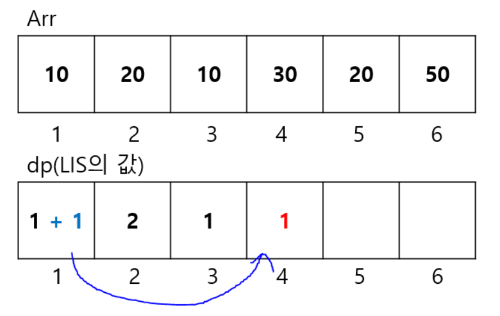
dp[0] + 1 인 값 2가 dp[3] 의 값 후보가 될 수 있다.
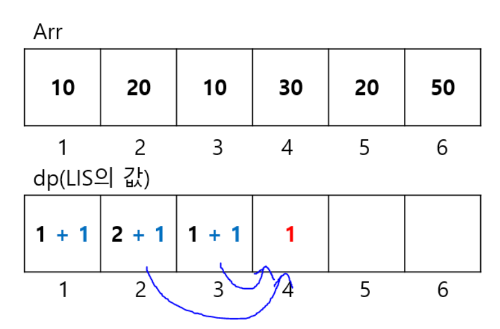
마찬가지로 두 번째 원소(20), 세 번째 원소(10)에 보다 네 번째 원소(30)은 크다. 부분 수열의 길이를 증가시킬 수 있으므로 dp[2] + 1 = 3, dp[3] + 1 = 2의 값을 dp[4]의 값 후보에 올릴 수 있다.
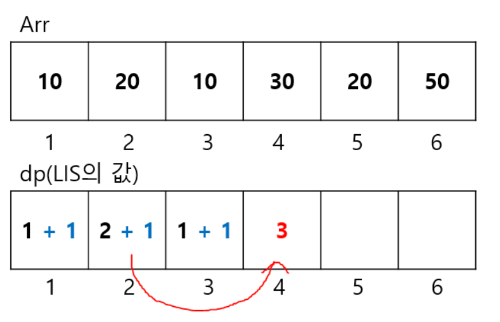
그렇다면, 이제 자기 자신의 길이 1과 첫 번째/두 번째/세 번째 원소에 대해 본인을 추가 시킨 LIS 의 길이 중 가장 큰 값은 무엇인가?
이는 2번째 원소로부터 본인의 길이를 추가시킨 3이 될 것임을 알 수 있다. 따라서 해당 위치의 dp 값은 3이 되는 것이다.
이러한 규칙으로 다섯 번째 원소 20을 생각해보자.
[ 원소 arr[4] = 20 ]

20이라는 값은 이전 원소들(10, 20, 10, 30)에 대하여 그 값이 10인 경우(첫 번째, 세 번째 원소)에 대해서만 부분 수열의 길이가 증가할 가능성이 있다. 따라서, 해당 위치의 LIS의 값에 본인의 길이를 + 1한 경우만 후보에 올라갈 수 있다.

후보(자기 자신의 길이 1, 그리고 2)중 2가 가장 크므로 dp[4] 는 2가 된다.
[ 원소 arr[5] = 50 ]
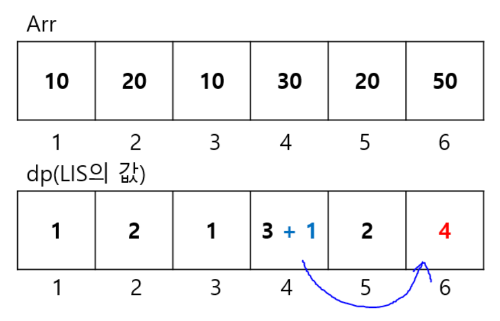
여섯 번째 원소 50인 경우, 원소 30의 LIS값인 3에 자기 자신 길이 1를 더한 후보인 4가 제일 크므로 dp[5]가 4가 된다.
2. 점화식 도출
(1) dp(= LIS 길이 )를 자기 자신의 길이인 1로 초기화 하기
dp[i] = 1
(2) 방문한 원소(arr[i])의 위치 이전의 원소들(arr[0]....arr[i-1])에 대하여 부분 수열의 길이가 증가할 가능성이 존재하는 경우, 해당 위치의 dp 테이블의 값에 +1(자기 자신의 길이)을 한 값들 중 가장 큰 값을 dp[i]로 설정
dp[i] = Math.max(dp[i], dp[j] +1)
-----> 즉, LIS 후보값 들 중 가장 큰 값을 채택
3. 구현
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.util.Arrays;
public class Main{
public static void main(String[] args)throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int[] arr = new int[n];
int[] dp = new int[n];
for(int i= 0; i<n; i++){
arr[i] = Integer.parseInt(st.nextToken());
dp[i] = 1; // 자기 자신의 길이 1로 dp 값(LIS길이) 미리 초기화
}
int max = 1;
for(int i = 1; i<n; i++){
for(int j = 0; j< i; j++ ){
if(arr[j] < arr[i]){
dp[i] = Math.max(dp[i],dp[j]+1);
}
}
if(dp[i] > max) max = dp[i]; //전체 수열에 대한 LIS 값 설정
}
System.out.println(max);
}
}
#참고 자료
'Coding Test > 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] 이분탐색(Binary Search)이란? (1) | 2024.10.02 |
|---|---|
| [알고리즘] 백트래킹이란? & 대표 문제: 백준 15679 N과M(1) - 자바 (0) | 2024.10.01 |
| [알고리즘 정리] DP(Dynamic Programming) : 동적 계획법 (1) | 2024.08.24 |
| [알고리즘] 그리디 알고리즘(탐욕법) 정리 (0) | 2024.08.20 |


